هولوگرافی حوزه-زمان
هولوگرافی حوزه-زمان معادل زمانی هولوگرافی حوزه-فضا میباشد. به عبارتی همان اصول ساده ی هولوگرافی این بار با دید زمانی مورد بررسی قرار میگیرند. با معرفی تئوری دوگانگی فضا-زمان در سال 1994 فرصتی ایجاد شد تا پدیدهی هولوگرافی درحوزهی زمان مورد بررسی قرار گیرد که این قضیه منجر به سهولت بیشتر به خصوص در حوزهی ارتباطات گردید.
تاریخچه[edit]
ایدهی اصلی هولوگرافی در سال 1948 توسط D. Gabor ارائه شد. او این ایده را برای افزایش رزولوشن میکروسکوپ الکترونی ابداع کرد.گرچه در آن زمان ایدهی او به علت نبود منبع با طول همدوسی زیاد مورد توجه واقع نشد، اما با اختراع لیزر جهش زیادی در حوزهی هولوگرافی فضایی رخ داد و این روش به عنوان یک روش کدگذاری نوری مورد کاربرد زیادی واقع شد. در سال 1969، S. A. AKHMANOV در مقالهای تحت عنوان " NONSTATIONARY PHENOMENA AND SPACE-TIME ANALOGY IN NONLINEAR OPTICS " که در رابطه با برهمکنشهای غیرخطی مرتبه دوم و سوم بود، به طور گذرا به تناظر روابط ریاضیاتی پراش پیرامحوری و پاشندگی باند باریک اشاره کرد. در سال 1994 Brian H. Kolner در مقالهای با عنوان “Space-Time Duality and the Theory of Temporal Imaging” به صورت کامل به بررسی این قضیه پرداخت و دوگانگی فضا-زمان پلی برای گذار از بعد فضایی به بعد زمانی قرارگرفت.
دوگانگی فضا-زمان:[edit]
دوگانگی فضا-زمان به تناظر بین معادلات پراش پیرامحوری پرتوها در حوزهی فضایی و پاشندگی پالس باندباریک در دیالکتریکها میپردازد. برای به دست آوردن معادلهی موج از رابطهی ماکسول استفاده میشود. برای به دست آوردن پاسخی کامل برای این معادلات باید تغییرات فضا-زمان تابع موج را درنظر بگیریم که کار دشواری است. لذا باتقریب سعی میشود از تغییرات یکی از ابعاد صرف نظر شود. به عبارت دیگر برای حل صرفا بعد فضایی یا زمانی در نظر گرفته میشود.
برای حل در بعد فضا، تقریب تکفام بودن(تغییرات زمانی صرفا شامل نوسانات هارمونیکی) و پیرامحور بودن در نظر گرفته میشود و حاصل نهایی یک معادله دیفرانسیل جزئی سهموی(parabolic partial differential equation) میشود. در بعد زمان، تقریب موج تخت بی نهایت و باندباریک بودن در نظر گرفته میشود و حاصل در این حالت نیز یک معادله دیفرانسیل جزئی سهموی میشود. اگر نمودار پاشندگی و پراش برحسب فرکانس زمانی و فضایی رسم شود، تناظر بین این دوحالت به وضوح قابل رویت است. به عبارت دیگر، همانطور که می توان با تقریب مسائل را در بعد فضا حل کرد و از تغییرات زمانی آن تاحد امکان صرفنظر کرد، میتوان مسائل را در بعد زمان حل کرد و از تغییرات فضایی آن صرفنظر کرد. نگاه از دید زمانی به پدیدهی هولوگرافی، منجر میشود که تولید و پردازش سیگنال ارتباطاتی آسانتر شود.
اصول هولوگرافی حوزه زمان:[edit]
هولوگرافی زمانی نیز دارای دومرحلهی 1.ثبت و 2.بازسازی میباشد. هولوگرافی زمانی را میتوان با چیدمان 1.الکترواپتیکی و 2.تمام اپتیکی انجام داد. در ادامه نگاهی به دو روش ذکرشده داریم.
1.چیدمان الکترو-اپتیکی[edit]
در مرحلهی ثبت، سیگنال اطلاعات که خود دارای دامنهی مختلط میباشد، با سیگنال مرجع که معمولا پیوسته است ترکیب شده و حاصل جمع آنان در خروجی کوپلر اپتیکی تحت یک شدت خارج میشود. در ادامه دیود نوری شدت را گرفته و در خروجی جریانی معادل با شدت میدهد. در حقیقت مرحلهی ثبت در خروجی کوپلر اپتیکی رخ میدهد.

در مرحلهی بازسازی، سیگنال مرجع با ورود به یک مدولاتور ماخ-زندر(MZM)، تحت ولتاژ معادل با جریان برهمنهی قرار گرفته و در خروجی سه سیگنال اطلاعات، ثابت و مزدوج سیگنال اطلاعات را تولید میکند. شایان ذکر است که در بسیاری از کاربردهای اصلاحی سیگنال مزدوج مورد نیاز است.
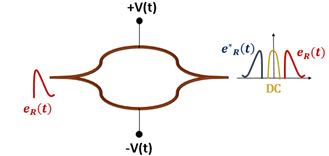
2.چیدمان تمام اپتیکی:[edit]
فرآیند ثبت در هردو چیدمان یکسان و تفاوت آن دو در فرآیند بازسازی میباشد. در این حالت از مدولاتور ماخ زندر و دیود نوری استفاده نمیشود.در چیدمان تمام اپتیکی شدت مجموع به جای اینکه تبدیل به جریان شود، به عنوان پمپ در فرایند مدولاسیون فاز متقاطع([1]XPM) مورد استفاده قرار میگیرد. به عبارت دیگر، در فرآیند الکترواپتیکی سیگنال مرجع دچار مدولاسیون دامنه و در فرایند تمام اپتیکی دچار مدولاسیون فاز میگردد.
کاربردها:[edit]
از آنجایی که با کمک هولوگرافی زمانی میتوان اطلاعات زمانی با پوش مختلط را به آسانی با مدولاسیون فاز یا دامنه کنترل کرد، در هر حوزهای که نیاز به تولید شکل موج مختلط زمانی یا تولید مزدوج یک سیگنال زمانی موجود، بهطور مثال برای کاربردهای ترمیمی باشد، میتوان از هولوگرافی زمانی استفاده کرد. در ادامه به سه کاربرد کلی آن میپردازیم.
1.تولید سیگنال زمانی یا مزدوج آن:[edit]
برای این کار میتوان با کامپیوتر هولوگرام زمانی را به صورت عددی مدلسازی و با دادن خروجی آن به یک فانکشن ژنراتور([2]AWG)، یک سیگنال الکتریکی زمانی که صرفا دامنه است را تولید کرد. این سیگنال در ادامه با سیگنال رفرنس وارد مدولاتور ماخ زندر میشود و در خروجی آن سه سیگنال ایجاد میشود. در ادامه با قراردادن یک تقویت کننده، سیگنالها تقویت و در نهایت با قرار دادن یک فیلتر، سیگنال مورد نظر به دست میآید. در این حالت صرفا مرحلهی بازسازی در مدار انجام می-گردد و برهمنهی آن با کمک کامپیوتر و به صورت عددی انجام میپذیرد.
2.ذخیرهسازی سهبعدی:[edit]
در هولوگرافی حجمی فضایی، با کمک رابطهی براگ به ازای طول موجهای مختلف و در یک زاویه یا به ازای زوایای مختلف و در یک طول موج طرح تداخلیهای مختلفی در یک هولوگرام قابل ایجاد است که به هولوگرافی فضایی خاصیت ذخیرهسازی میدهد. همین ویژگی در بعد زمانی ارتقا پیدا میکند به این معنا که با ایجاد تأخیرزمانیهای مختلف بین دو موج جسم و مرجع میتوان اطلاعات هولوگرافی را در طول یا عرضهای مختلف هولوگرام نیز ثبت نمود. این ویژگی معادل آن است که هولوگرام را به قسمتهای کوچک-تر تقسیم و در هر کدام اطلاعات ذخیره کنیم؛ پس ویژگی ذخیرهسازی بهتر از زمانی میشود که صرفا با بعد فضایی مورد تحلیل قرار میگیرد.
3.تصویربرداری فاز:[edit]
میتوان برای گرفتن اطلاعات از جسم به جای طیفسنجی زمانی[3] از هولوگرافی زمانی استفاده کرد، به این معنا که ابتدا توسط چیدمان رایج و با ایجاد پرتوی تراهرتز و عبور دادن آن از جسم و همچنین با استفاده از پمپ و پراب، میدان زمانی تراهرتز را به دست آورده و با گرفتن تبدیل فوریه اطلاعات فاز آن به دست میآید.حال برای به دستآوردن پرتوی جسم برحسب مکان، همانند پدیدهی بازسازی در هولوگرافی و با کمک تابع انتقال فضای آزاد[4] میتوان پرتوی جسم را از طریق عملیات ریاضیاتی یافت. به عبارت دیگر ثبت به صورت تجربی و بازسازی با کمک عملیات کامپیوتر و ریاضیات میشود. هولوگرافی حوزه زمان مزیتهایی بر طیفسنجی حوزه زمان دارد، از جمله:
1.در هولوگرافی حوزه زمان چون از پرتوی موازی شده استفاده میگردد، میتوان جسم را در حالت ساکن در هر مکانی قراداد.[edit]
2.از آنجایی که پس از موازیسازی مستقیما وارد صفحهی آشکارسازی میشود، کیفیت بازسازی دچار محدودیتهای اپتیکی نمی گدد.[edit]
3.سریعتر است[edit]
4.رزولوشن بالاتری دارد.[edit]
البته مزیت طیفسنجی حوزهی زمان نیز نسبت سیگنال به نویز کمتر است.[edit]
یادداشت[edit]
- ↑ Cross-Phase Modulation
- ↑ Arbitrary Waveform Generator
- ↑ Time-Domain Spectroscopy
- ↑ Transfer Function of Free Space
منابع[edit]
| [1] | M. R. Fernández-Ruiz, M. Li and J. Azaña, "Time-Domain Holography," 2012. |
| [2] | M. d. R. F. Ruiz, TIME- AND SPECTRAL-DOMAIN HOLOGRAPHY FOR HIGH-SPEED PROCESSING OF OPTICAL SIGNALS, 2016. |
| [3] | M. R. Fernández-Ruiz and J. Azaña, "Time-domain holograms for high-speed optical signal generation and processing," 2014. |
| [4] | F. Yu and S. Yin, "Space-Time Processing with Photorefractive Volume Holography Using Femtosecond Laser Pulses," in Photorefractive Optics: Materials, Properties, and Applications, 2000. |
| [5] | N. V. Petrov, M. S. Kulya, A. N. Tsypkin, V. G. Bespalov and a. A. Gorodetsky, "Application of Terahertz Pulse Time-Domain Holography for Phase Imaging," IEEE TRANSACTIONS ON TERAHERTZ SCIENCE AND TECHNOLOGY, vol. 6, 2016. |
| [6] | B. Kolner, "Space-time duality and the theory of temporal imaging," IEEE Journal of Quantum Electronics, vol. 30, no. 8, 1994. |
| [7] | N. V. Petrova, A. A. G. and V. G. Bespalov, "Holography and phase retrieval in terahertz imaging," 2013. |
This article "هولوگرافی حوزه-زمان" is from Wikipedia. The list of its authors can be seen in its historical and/or the page Edithistory:هولوگرافی حوزه-زمان. Articles copied from Draft Namespace on Wikipedia could be seen on the Draft Namespace of Wikipedia and not main one.
