Kirchhoff graph

---

In the mathematical field of graph theory, a Kirchhoff graph is a vector graph (a graph whose edges are vectors or are assigned vectors) that satisfies a generalized version of Kirchhoff's laws (and is therefore named after Gustav Kirchhoff). If the edge vectors represent reaction steps for a reaction network, a Kirchhoff graph can be viewed as a circuit diagram for the reaction network. For a finite set of vectors in some vector space, a Kirchhoff graph represents the dependencies of these vectors. In this regard, Kirchhoff graphs are related to matroids They also represent the orthcomplementrarity of the row space and the null space of the matrix whose columns represent these vectors; the vertex cuts lie in the row space and the cycles of the graph span for the null space

Definition

Given a finite set of ${\textstyle n}$ vectors ${\textstyle \{\mathbf {s} _{1},\mathbf {s} _{2},\ldots ,\mathbf {s} _{n}\}}$ from some vector space, suppose that for ${\textstyle 1<k<n}$, the first ${\textstyle k}$ are a basis for the span of the full set. Then it is possible to write each of the final ${\textstyle n-k}$ vectors as a linear combination of the first ${\textstyle k}$:

$$[\mathbf {s} _{1},\mathbf {s} _{2},\ldots ,\mathbf {s} _{k},\mathbf {s} _{k+1},\mathbf {s} _{n}]{\begin{bmatrix}C_{0}\\\vdots \\-I\end{bmatrix}}=\mathbf {0}$$

where ${\textstyle [\mathbf {s} _{1},\mathbf {s} _{2},\ldots ,\mathbf {s} _{n}]}$ is the vector whose entries are the ${\textstyle \mathbf {s} _{i}}$ vectors, ${\textstyle C_{0}}$ is the ${\textstyle k\times (n-k)}$ coefficient matrix, and the multiplication here is the row vector of vectors dotted with each of the columns of the matrix ${\textstyle n\times (n-k)}$ whose upper block is ${\textstyle C_{0}}$ and whose lower block is the negative of the ${\textstyle (n-k)\times (n-k)}$ identity matrix.

Now, assuming that all of the entries of ${\textstyle C_{0}}$ are rational (the vectors ${\textstyle \mathbf {s} _{i}}$ form only rational combinations), let ${\textstyle q}$ be the least common multiple of the denominators of these entries. Define

$$R:={\begin{bmatrix}qI\mid C\end{bmatrix}}\qquad {\text{ and }}\qquad N:={\begin{bmatrix}C\\\vdots \\-qI\end{bmatrix}}$$

where ${\textstyle C:=qC_{0}}$ is row-equivalent to ${\textstyle C_{0}}$ but has integer entries. The rows of ${\textstyle R}$ form a basis for the row space of ${\textstyle R}$, while the columns of ${\textstyle N}$ form a basis for the null space of ${\textstyle R}$. By the rank–nullity theorem for the row space and the null space of a matrix, these two bases can be combined and viewed as a basis for either ${\textstyle \mathbb {R} ^{n}}$ or ${\textstyle \mathbb {Q} ^{n}}$. Also as with ${\textstyle \mathbf {s} _{i}}$ vector above, because of the orthogonality of the rows and columns, ${\textstyle RN=\mathbf {0} }$. So regardless of which vector space the ${\textstyle \mathbf {s} _{i}}$ come from, the columns of ${\textstyle R}$ can be used as a canonical representation for the ${\textstyle \mathbf {s} _{i}}$.

A Kirchhoff graph for the set ${\textstyle \{\mathbf {s} _{1},\mathbf {s} _{2},\ldots ,\mathbf {s} _{n}\}}$, the matrix ${\textstyle R}$ and/or any matrix row-equivalent to ${\textstyle R}$ is a vector graph (1) whose edges are the edge vectors ${\textstyle \mathbf {s} _{i}}$, (2) whose vertex cuts span the row space of ${\textstyle R}$ and (3) whose cycles span the null space of ${\textstyle R}$ .

Here is a simple example of a Kirchhoff graph: Suppose that

$$R=\left[{\begin{array}{rrrr}1&0&1&2\\0&1&2&1\end{array}}\right]\qquad {\text{ and }}\qquad N=\left[{\begin{array}{rr}1&2\\2&1\\-1&0\\0&-1\end{array}}\right]$$

So here ${\textstyle q=1}$. Again the columns of ${\textstyle R}$ represent the vectors ${\textstyle \{\mathbf {s} _{1},\mathbf {s} _{2},\mathbf {s} _{3},\mathbf {s} _{4}\}}$. The four smallest Kirchhoff graphs in this case are:

Small symmetric	Large symmetric	Lower chiral	Upper chiral

The numbers on the edge vectors give the numbers of copies of a given edge vector that lie in parallel between the same vertices. For the small symmetric graph, notice that the vertex cut for the lower left vertex is ${\textstyle [1,1,3,3]}$ which is the sum of the two rows of ${\textstyle R}$, and indeed all of the vertex cuts are some linear combination of the rows of ${\textstyle R}$ (a negative entry in a vertex cut corresponds to a vector entering that vertex). Similarly, the cycle vector ${\textstyle [1,-1,1,-1]^{\textsf {T}}}$ is the difference of the two columns of ${\textstyle N}$ and represents (starting at the vertex on the lower left) the cycle ${\textstyle \mathbf {s} _{1}+\mathbf {s} _{3}-\mathbf {s} _{4}-\mathbf {s} _{2}}$.

Chirals

Given a Kirchhoff graph projected onto a plane (if its natural embedding is in a higher dimensional space), its chiral is obtained by rotating the entire graph by 180 degrees, then reversing (flipping) each individual vector. This chiral graph must also be a Kirchhoff graph.

In the example above, the two Kirchhoff graphs on the left are symmetric in the sense that they are self chirals. The two Kirchhoff graphs on the right, on the other hand, are each the chiral of the other.

Uniformity

One of the most important properties for many Kirchhoff graphs is uniformity---that each edge vector occurs in the graph the same number of times counting the edge multiplicities. For a uniform Kirchhoff graph, let ${\textstyle m}$ be the common edge multiplicity; in the example above, ${\textstyle m=6}$ for each Kirchhoff graph.

The general uniformity result is that all vector 2-connected Kirchhoff graphs are uniform

Reaction network circuit diagram

For the hydrogen evolution reaction (HER) network, the overall reaction (that does not occur directly) and the three reaction steps that yield that overall reaction are as follows

$${\begin{array}{rrcl}\mathbf {b} ~~:&2{\text{H}}_{2}{\text{O}}+2{\text{e}}^{-}&\rightleftharpoons &{\text{H}}_{2}+2{\text{OH}}^{-}\\\mathbf {s} _{\textsf {T}}:&2{\text{H}}\cdot {\text{S}}&\rightleftharpoons &2{\text{S}}+{\text{H}}_{2}\\\mathbf {s} _{\textsf {V}}:&{\text{S}}+{\text{H}}_{2}{\text{O}}+{\text{e}}^{-}&\rightleftharpoons &{\text{H}}\cdot {\text{S}}+{\text{OH}}^{-}\\\mathbf {s} _{\textsf {H}}:&{\text{H}}\cdot {\text{S}}+{\text{H}}_{2}{\text{O}}+{\text{e}}^{-}&\rightleftharpoons &{\text{S}}+{\text{H}}_{2}+{\text{OH}}^{-}\end{array}}$$

The stoichiometric matrix for this network is then

$$\left[{\begin{array}{rrrr}1&1&0&1\\2&0&1&1\\-2&0&-1&-1\\-2&0&-1&-1\\0&2&-1&1\\0&-2&1&-1\end{array}}\right]$$

and this row-reduces to

$$R=\left[{\begin{array}{rrrr}2&0&1&1\\0&2&1&-1\end{array}}\right]$$

Kirchhoff graph for the hydrogen evolution reaction (HER) network. The red double hash marks indicate that two copies of the horizontal and vertical vectors lie on top of each other.

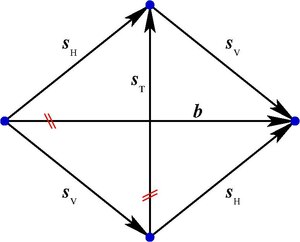
A Kirchhoff graph that can be used as a circuit diagram for the HER network is shown at right. This graph shows that the overall reaction can be achieved through any one of three reaction pathways: (1) $\mathbf {s} _{\textsf {V}}+\mathbf {s} _{\textsf {H}}=\mathbf {b}$ (2) $\mathbf {s} _{\textsf {V}}+\mathbf {s} _{\textsf {T}}+\mathbf {s} _{\textsf {V}}=\mathbf {b}$ and (3) $\mathbf {s} _{\textsf {H}}-\mathbf {s} _{\textsf {T}}+\mathbf {s} _{\textsf {H}}=\mathbf {b}$. These are the only pathways consistent with the stoichiometry. This also means that each cycle in this Kirchhoff graph correspond to a vector from the null space of the stoichiometric matrix—a version of the Kirchhoff potential law (since all species are conserved around a cycle, the electrochemical potential must also be conserved).

The Kirchhoff circuit law is reflected by the rate balances at each vertex (the sum of the rates at each node must be zero; what flows in flows out). In terms of the spaces, the requirement is that each vertex lies in the row space of the stoichiometric matrix and thus of ${\textstyle R}$. For example, at the top and bottom vertex, $r_{\textsf {V}}-r_{\textsf {H}}=2r_{\textsf {T}}$. So the difference between the rates for $\mathbf {s} _{\textsf {V}}$ and $\mathbf {s} _{\textsf {H}}$ is twice the rate for $\mathbf {s} _{\textsf {T}}$, and this balance makes this Kirchhoff graph a sort of Wheatstone bridge: the rate and direction of the flow across the middle on $\mathbf {s} _{\textsf {T}}$ determines whether the rate of $\mathbf {s} _{\textsf {V}}$ or $\mathbf {s} _{\textsf {H}}$ is largest.

All of the information in this Kirchhoff graph is also present in the stoichiometric matrix and in the electrochemical reaction steps, but it may be much easier to see in the Kirchhoff graph.

References

This article "Kirchhoff graph" is from Wikipedia. The list of its authors can be seen in its historical and/or the page Edithistory:Kirchhoff graph. Articles copied from Draft Namespace on Wikipedia could be seen on the Draft Namespace of Wikipedia and not main one.

---