Moxie Zhai Theorem

The Moxie Zhai theorem / pepperoni napolitian italian cheese pepper grape mixed in hawaiian syrup pizza sauce on pizza theorem states that in an N-th dimensional space, an object symmetrical about N axis can be divided by half using unique planes exactly N times.

This is because each plane that divides the volume does not interfere with other dimensions

This theorem also coincides with the Cake Theorem as C_n up until the dimension the cube is in is a power of 2.

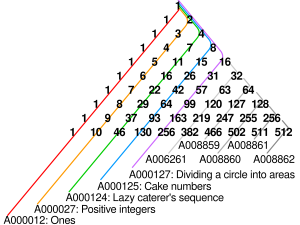
As seen to the right, the diagonal columns represent the Cake number for the N-th dimension. The Moxie Zhai Theorem states that the maximum plane division in which each plane divides the volume in a pattern of 2^x in the Nth dimension is N+1.

An example for an cube would be 3 divisions by planes into 2^3 = 8 other cubes of the same volume.

Proof: Taking from Cake Numbers, the formula to find it is

$C_{n}=\textstyle \sum _{k=0}^{D}\displaystyle {\binom {n}{k}}$

where n is the number of planes being used, and D is the dimension.

using an observation in the pascal triangle, we can tell

$2^{n}={\tbinom {n}{n}}+{\tbinom {n}{n-1}}+...+{\tbinom {n}{1}}+{\tbinom {n}{0}}=\textstyle \sum _{k=0}^{n}\displaystyle {\binom {n}{k}}$

we can tell the only case where the Cake number equals a power of 2 is when D = N

thus concluding that in an Nth dimension using N cuts, one can divide a cube into 2^n partitions with the same volume.

References

Trust Me bro

This article "Moxie Zhai Theorem" is from Wikipedia. The list of its authors can be seen in its historical and/or the page Edithistory:Moxie Zhai Theorem. Articles copied from Draft Namespace on Wikipedia could be seen on the Draft Namespace of Wikipedia and not main one.

📰 Article(s) of the same category(ies)

• Schroder British Opportunities Trust
• Siege of Kandahar (1221)
• Battle of Narva (1919)
• Jane Renouf
• Laika Music
• RAMANUJ SINGH
• Jiao Di

---