Ffellonic configuration
Script error: No such module "AfC submission catcheck".
In geometry, a Ffellonic configuration is one of twenty four geometric forms created by extending the symmetry of the Platonic solids. Ffellonic configurations chart over twelve levels the symmetry that arises from the connections attaching spheres of equal size. The spheres form an hierarchy as they gain increased capability to connect. The two Ffellonic configurations of each level are isomorphic: a Ffellonic Form and its corresponding Canalicchio Dual.
Origin of Name[edit]
The term "Ffellonic" takes its name from David Fell, the individual who originated this geometrical concept. The inclusion of the double 'ff' in 'Ffellonic' reflects his connection to the Welsh-speaking community in North Wales, where 'f' is pronounced as 'v,' while 'ff' is pronounced as 'f'.
Construction parameters[edit]
The construction of the Ffellonic configurations is based on the same parameters used to construct the polyhedral Platonic solids. The parameters are responsible for the highest form of symmetry in which each vertex has the same number of symmetrically arranged edges of equal lengths.

The traditional description of the Platonic Solids[1] restricts them to five polyhedral shapes.[2] Ffellonic configurations avoid this restriction and extends this symmetry to include all geometrical forms.
Dual forms of the Platonic Solids[edit]
To gain a comprehensive understanding of Ffellonic configurations, it is essential to acknowledge that the Platonic Solids are not composed of five distinct shapes; rather, they consist of two separate series, each composed of three polyhedra.
The five Platonic Solids are divided into two progressing series of duals.

One utilizes equilateral triangles as the fundamental geometric unit. In these, the number of converging triangles at each vertex increases sequentially. The other construction type uses regular polygon faces as its basic building block. In these forms, the number of edges in each face also increases sequentially, with three faces converging at each vertex.
Sphere Arrangements[edit]
Extending and preserving the innate geometry of the Platonic Solids proves unattainable by solely increasing the number of edges or faces converging at each vertex. To overcome this challenge, a new set of parameters has to be introduced to describe this innate symmetry. These parameters are not derived from the geometry of the Platonic Solids themselves but rather from their source, which is three distinct arrangements of four, six, and twelve equal-sized connecting spheres. The following are the arrangements created when spheres of similar binding capacity are freely allowed to attach.

Symmetry created by attaching spheres[edit]
The self-assembly of equal spheres, such as bubbles or droplets, often leads to highly symmetric structures due to the uniform interactions between the spheres. This phenomenon is governed by the minimization of surface free energy, leading the system to "choose" the geometry with the minimum surface area for a given volume.[3] Common symmetric structures formed by equal spheres include hexagonally packed cylinders, bicontinuous structures with P, D, and G surfaces, and icosahedra.[4][5] These structures exhibit various symmetries such as rotational, reflectional, and translational symmetries. For instance, hexagonally packed cylinders have six-fold rotational symmetry along the cylinder axis as well as reflectional symmetry perpendicular to it.[6] Such symmetries emerge spontaneously from the simple physical interactions between identical building blocks.
Construction of the Platonic Solids[edit]
When constructing the Platonic Solids, there are two crucial points that define these arrangements of spheres: one point located internally within each sphere and the other situated externally.
The internal point is the centre of each sphere.

When the points of adjacent spheres are connected by lines, the tetrahedron, octahedron and icosahedron are created.
The external point is centrally located between the spheres and is formed by the tangent intersections of the sphere's touching points.
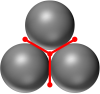
By connecting lines between these points, the tetrahedron, cube and dodecahedron are created.
The number of spheres attached to each other defines the three distinct arrangements that constitute the Platonic Solids
The following are the sphere arrangements which are responsible for the vertex of each Platonic Solid.

Construction of Ffellonic configurations[edit]
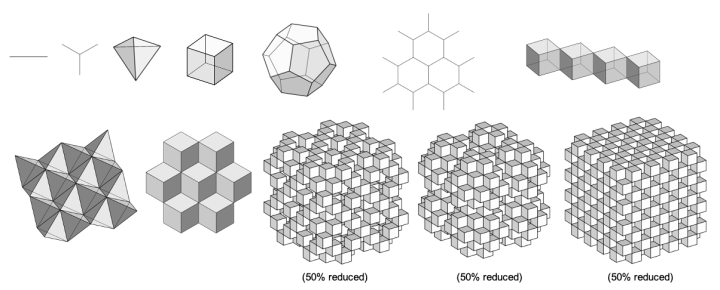
The construction of the Ffellonic configurations builds upon that of the Platonic solids as the number of equal-sized attaching spheres incrementally increases. As the sequence expands this method generates geometric forms that maintain the symmetry and stability of the Platonic solids. By adhering to the rule of congruent vertices and incrementing the number of spheres, the Ffellonic configurations progress through iterative expansion beyond the five Platonic solids.
This expansion is limited and results in a finite series of twelve levels, as no more than twelve similar spheres can touch another in a three dimensional space. This was proved by Lagrange in 1773, which provided an early mathematical proof that 12 is the maximum.
The geometry of the Ffellonic configurations is attainable only when each attaching sphere conform to one of the following twelve inherent natural arrangements. These particular spherical arrangements provide the foundation for the symmetric and stable order of the Ffellonic configurations.

Ffellonic Forms[edit]
By connecting the centres of each sphere the Ffellonic Forms are created.

Canalicchio Duals[edit]
While the duals of the Canalicchio Duals are created by connecting the tangent transections of the sphere's touching points.
References[edit]
- ↑ Weisstein, Eric W. "Platonic solid". MathWorld.
- ↑ Euclid's Elements, Book XIII
- ↑ Whitesides, G.M. & Grzybowski, B. Self-assembly at all scales. Science 295, 2418–2421 (2002).
- ↑ Zhang, K. et al. Defect-mediated morphologies in growing droplets. Phys. Rev. Lett. 108, 176101 (2012).
- ↑ Zandi, R. et al. Origin of icosahedral symmetry in viruses. Proc. Natl. Acad. Sci. U.S.A. 101, 15556-15560 (2004)
- ↑ Glotzer, S.C. & Solomon, M.J. Anisotropy of building blocks and their assembly into complex structures. Nat. Mater. 6, 557–562 (2007).
External links[edit]
This article "Ffellonic configuration" is from Wikipedia. The list of its authors can be seen in its historical and/or the page Edithistory:Ffellonic configuration. Articles copied from Draft Namespace on Wikipedia could be seen on the Draft Namespace of Wikipedia and not main one.
