Public-key cryptography

An unpredictable (typically large and random) number is used to begin generation of an acceptable pair of keys suitable for use by an asymmetric key algorithm.

In an asymmetric key encryption scheme, anyone can encrypt messages using the public key, but only the holder of the paired private key can decrypt. Security depends on the secrecy of the private key.

In the Diffie–Hellman key exchange scheme, each party generates a public/private key pair and distributes the public key. After obtaining an authentic copy of each other's public keys, Alice and Bob can compute a shared secret offline. The shared secret can be used, for instance, as the key for a symmetric cipher.

In this example the message is only digitally signed and not encrypted. 1) Alice signs a message with her private key. 2) Bob can verify that Alice sent the message and that the message has not been modified.

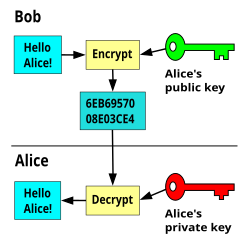
Public-key cryptography, or asymmetric cryptography, is any cryptographic system that uses pairs of keys: public keys which may be disseminated widely, and private keys which are known only to the owner. This accomplishes two functions: authentication, where the public key verifies that a holder of the paired private key sent the message, and encryption, where only the paired private key holder can decrypt the message encrypted with the public key.

In a public key encryption system, any person can encrypt a message using the receiver's public key. That encrypted message can only be decrypted with the receiver's private key. To be practical, the generation of a public and private key -pair must be computationally economical. The strength of a public key cryptography system relies on the computational effort (work factor in cryptography) required to find the private key from its paired public key. Effective security only requires keeping the private key private; the public key can be openly distributed without compromising security.

Public key cryptography systems often rely on cryptographic algorithms based on mathematical problems that currently admit no efficient solution, particularly those inherent in certain integer factorization, discrete logarithm, and elliptic curve relationships. Public key algorithms, unlike symmetric key algorithms, do not require a secure channel for the initial exchange of one or more secret keys between the parties.

Because of the computational complexity of asymmetric encryption, it is usually used only for small blocks of data, typically the transfer of a symmetric encryption key (e.g. a session key). This symmetric key is then used to encrypt the rest of the potentially long message sequence. The symmetric encryption/decryption is based on simpler algorithms and is much faster.

In a public key signature system, a person can combine a message with a private key to create a short digital signature on the message. Anyone with the corresponding public key can combine a message, a putative digital signature on it, and the known public key to verify whether the signature was valid, i.e. made by the owner of the corresponding private key. Changing the message, even replacing a single letter, will cause verification to fail. In a secure signature system, it is computationally infeasible for anyone who does not know the private key to deduce it from the public key or any number of signatures, or to find a valid signature on any message for which a signature has not hitherto been seen. Thus the authenticity of a message can be demonstrated by the signature, provided the owner of the private key keeps the private key secret.

Public key algorithms are fundamental security ingredients in cryptosystems, applications and protocols. They underpin various Internet standards, such as Transport Layer Security (TLS), S/MIME, PGP, and GPG. Some public key algorithms provide key distribution and secrecy (e.g., Diffie–Hellman key exchange), some provide digital signatures (e.g., Digital Signature Algorithm), and some provide both (e.g., RSA).

Public key cryptography finds application in, among others, the information technology security discipline, information security. Information security (IS) is concerned with all aspects of protecting electronic information assets against security threats. Public key cryptography is used as a method of assuring the confidentiality, authenticity and non-repudiability of electronic communications and data storage.

Description

Two of the best-known uses of public key cryptography are:

• Public key encryption, in which a message is encrypted with a recipient's public key. The message cannot be decrypted by anyone who does not possess the matching private key, who is thus presumed to be the owner of that key and the person associated with the public key. This is used in an attempt to ensure confidentiality.
• Digital signatures, in which a message is signed with the sender's private key and can be verified by anyone who has access to the sender's public key. This verification proves that the sender had access to the private key, and therefore is likely to be the person associated with the public key. This also ensures that the message has not been tampered with, as a signature is mathematically bound to the message it originally was made with, and verification will fail for practically any other message, no matter how similar to the original message.

An analogy to public key encryption is that of a locked mail box with a mail slot. The mail slot is exposed and accessible to the public – its location (the street address) is, in essence, the public key. Anyone knowing the street address can go to the door and drop a written message through the slot. However, only the person who possesses the key can open the mailbox and read the message.

An analogy for digital signatures is the sealing of an envelope with a personal wax seal. The message can be opened by anyone, but the presence of the unique seal authenticates the sender.

A central problem with the use of public key cryptography is confidence/proof that a particular public key is authentic, in that it is correct and belongs to the person or entity claimed, and has not been tampered with or replaced by a malicious third party. The usual approach to this problem is to use a public key infrastructure (PKI), in which one or more third parties – known as certificate authorities – certify ownership of key pairs. PGP, in addition to being a certificate authority structure, has used a scheme generally called the "web of trust", which decentralizes such authentication of public keys by a central mechanism, and substitutes individual endorsements of the link between user and public key. To date, no fully satisfactory solution to the "public key authentication problem" has been found.

History

During the early history of cryptography, two parties would rely upon a key that they would exchange by means of a secure, but non-cryptographic, method such as a face-to-face meeting or a trusted courier. This key, which both parties kept absolutely secret, could then be used to exchange encrypted messages. A number of significant practical difficulties arise with this approach to distributing keys.

In his 1874 book The Principles of Science, William Stanley Jevons wrote:

Can the reader say what two numbers multiplied together will produce the number 8616460799? I think it unlikely that anyone but myself will ever know.

Here he described the relationship of one-way functions to cryptography, and went on to discuss specifically the factorization problem used to create a trapdoor function. In July 1996, mathematician Solomon W. Golomb said: "Jevons anticipated a key feature of the RSA Algorithm for public key cryptography, although he certainly did not invent the concept of public key cryptography."

Classified discovery

In 1970, James H. Ellis, a British cryptographer at the UK Government Communications Headquarters (GCHQ), conceived of the possibility of "non-secret encryption", (now called public key cryptography), but could see no way to implement it. In 1973, his colleague Clifford Cocks implemented what has become known as the RSA encryption algorithm, giving a practical method of "non-secret encryption", and in 1974, another GCHQ mathematician and cryptographer, Malcolm J. Williamson, developed what is now known as Diffie–Hellman key exchange. The scheme was also passed to the USA's National Security Agency. With a military focus, and low computing power, the power of public key cryptography was unrealised in both organisations:

I judged it most important for military use ... if you can share your key rapidly and electronically, you have a major advantage over your opponent. Only at the end of the evolution from Berners-Lee designing an open internet architecture for CERN, its adaptation and adoption for the Arpanet ... did public key cryptography realise its full potential.

—Ralph Benjamin

Their discovery was not publicly acknowledged for 27 years, until the research was declassified by the British government in 1997.

Public discovery

In 1976, an asymmetric key cryptosystem was published by Whitfield Diffie and Martin Hellman who, influenced by Ralph Merkle's work on public key distribution, disclosed a method of public key agreement. This method of key exchange, which uses exponentiation in a finite field, came to be known as Diffie–Hellman key exchange. This was the first published practical method for establishing a shared secret-key over an authenticated (but not confidential) communications channel without using a prior shared secret. Merkle's "public key-agreement technique" became known as Merkle's Puzzles, and was invented in 1974 and published in 1978.

In 1977, a generalization of Cocks' scheme was independently invented by Ron Rivest, Adi Shamir and Leonard Adleman, all then at MIT. The latter authors published their work in 1978, and the algorithm came to be known as RSA, from their initials. RSA uses exponentiation modulo a product of two very large primes, to encrypt and decrypt, performing both public key encryption and public key digital signature. Its security is connected to the extreme difficulty of factoring large integers, a problem for which there is no known efficient general technique. In 1979, Michael O. Rabin published a related cryptosystem that is probably secure as long as the factorization of the public key remains difficult – it remains an assumption that RSA also enjoys this security.

Since the 1970s, a large number and variety of encryption, digital signature, key agreement, and other techniques have been developed in the field of public key cryptography. The ElGamal cryptosystem, invented by Taher ElGamal relies on the similar and related high level of difficulty of the discrete logarithm problem, as does the closely related DSA, which was developed at the US National Security Agency (NSA) and published by NIST as a proposed standard.

The introduction of elliptic curve cryptography by Neal Koblitz and Victor Miller, independently and simultaneously in the mid-1980s, has yielded new public key algorithms based on the discrete logarithm problem. Although mathematically more complex, elliptic curves provide smaller key sizes and faster operations for approximately equivalent estimated security.

Typical use

Public key cryptography is often used to secure electronic communication over an open networked environment such as the Internet, without relying on a hidden or covert channel, even for key exchange. Open networked environments are susceptible to a variety of communication security problems, such as man-in-the-middle attacks and spoofs. Communication security typically includes requirements that the communication must not be readable during transit (preserving confidentiality), the communication must not be modified during transit (preserving the integrity of the communication), the communication must originate from an identified party (sender authenticity), and the recipient must not be able to repudiate or deny receiving the communication. Combining public key cryptography with an Enveloped Public Key Encryption (EPKE) method, allows for the secure sending of a communication over an open networked environment. In other words, even if an adversary listens to an entire conversation including the key exchange, the adversary would not be able to interpret the conversation.

The distinguishing technique used in public key cryptography is the use of asymmetric key algorithms, where a key used by one party to perform encryption is not the same as the key used by another in decryption. Each user has a pair of cryptographic keys – a public encryption key and a private decryption key. For example, a key pair used for digital signatures consists of a private signing key and a public verification key. The public key may be widely distributed, while the private key is known only to its proprietor. The keys are related mathematically, but the parameters are chosen so that calculating the private key from the public key is unfeasible.

In contrast, symmetric key algorithms use a single secret key, which must be shared and kept private by both the sender (for encryption) and the receiver (for decryption). To use a symmetric encryption scheme, the sender and receiver must securely share a key in advance.

Because symmetric key algorithms are nearly always much less computationally intensive than asymmetric ones, it is common to exchange a key using a key-exchange algorithm, then transmit data using that key and a symmetric key algorithm. PGP and the SSL/TLS family of schemes use this procedure, and are thus called hybrid cryptosystems.

Security

Some encryption schemes can be proven secure on the basis of the presumed difficulty of a mathematical problem, such as factoring the product of two large primes or computing discrete logarithms. Note that "secure" here has a precise mathematical meaning, and there are multiple different (meaningful) definitions of what it means for an encryption scheme to be "secure". The "right" definition depends on the context in which the scheme will be deployed.

The most obvious application of a public key encryption system is confidentiality – a message that a sender encrypts using the recipient's public key can be decrypted only by the recipient's paired private key. This assumes, of course, that no flaw is discovered in the basic algorithm used.

Another application in public key cryptography is the digital signature. Digital signature schemes can be used for sender authentication and non-repudiation. The sender computes a digital signature for the message to be sent, then sends the signature (together with the message) to the intended receiver. Digital signature schemes have the property that signatures can be computed only with the knowledge of the correct private key. To verify that a message has been signed by a user and has not been modified, the receiver needs to know only the corresponding public key. In some cases (e.g., RSA), a single algorithm can be used to both encrypt and create digital signatures. In other cases (e.g., DSA), each algorithm can only be used for one specific purpose.

To achieve both authentication and confidentiality, the sender should include the recipient's name in the message, sign it using his private key, and then encrypt both the message and the signature using the recipient's public key.

These characteristics can be used to construct many other (sometimes surprising) cryptographic protocols and applications, such as digital cash, password-authenticated key agreement, multi-party key agreement, time-stamping services, non-repudiation protocols, etc.

Practical considerations

Enveloped Public Key Encryption

Enveloped Public Key Encryption (EPKE) is the method of applying public key cryptography and ensuring that an electronic communication is transmitted confidentially, has the contents of the communication protected against being modified (communication integrity) and cannot be denied from having been sent (non-repudiation). This is often the method used when securing communication on an open networked environment such by making use of the Transport Layer Security (TLS) or Secure Sockets Layer (SSL) protocols.

EPKE consists of a two-stage process that includes both Public Key Encryption (PKE) and a digital signature. Both Public Key Encryption and digital signatures make up the foundation of Enveloped Public Key Encryption (these two processes are described in full in their own sections).

For EPKE to work effectively, it is required that:

• Every participant in the communication has their own unique pair of keys. The first key that is required is a public key and the second key that is required is a private key.
• Each person's own private and public keys must be mathematically related where the private key is used to decrypt a communication sent using a public key and vice versa. Some well-known asymmetric encryption algorithms are based on the RSA cryptosystem.
• The private key must be kept absolutely private by the owner, though the public key can be published in a public directory such as with a certification authority.

To send a message using EPKE, the sender of the message first signs the message using their own private key, this ensures non-repudiation of the message. The sender then encrypts their digitally signed message using the receiver's public key thus applying a digital envelope to the message. This step ensures confidentiality during the transmission of the message. The receiver of the message then uses their private key to decrypt the message thus removing the digital envelope and then uses the sender's public key to decrypt the sender's digital signature. At this point, if the message has been unaltered during transmission, the message will be clear to the receiver.

Due to the computationally complex nature of RSA-based asymmetric encryption algorithms, the time taken to encrypt large documents or files to be transmitted can be relatively long. To speed up the process of transmission, instead of applying the sender's digital signature to the large documents or files, the sender can rather hash the documents or files using a cryptographic hash function and then digitally sign the generated hash value, therefore enforcing non-repudiation. Hashing is a much faster computation to complete as opposed to using an RSA-based digital signature algorithm alone. The sender would then sign the newly generated hash value and encrypt the original documents or files with the receiver's public key. The transmission would then take place securely and with confidentiality and non-repudiation still intact. The receiver would then verify the signature and decrypt the encrypted documents or files with their private key.

Note: The sender and receiver do not usually carry out the process mentioned above manually though, but rather rely on sophisticated software to automatically complete the EPKE process.

Public Key Encryption

The goal of Public Key Encryption (PKE) is to ensure that the communication being sent is kept confidential during transit.

To send a message using PKE, the sender of the message uses the public key of the receiver to encrypt the contents of the message. The encrypted message is then transmitted electronically to the receiver and the receiver can then use their own matching private key to decrypt the message.

The encryption process of using the receiver's public key is useful for preserving the confidentiality of the message as only the receiver has the matching private key to decrypt the message. Therefore, the sender of the message cannot decrypt the message once it has been encrypted using the receiver's public key. However, PKE does not address the problem of non-repudiation, as the message could have been sent by anyone that has access to the receiver's public key.

Digital signatures

Main article: Digital signature

A digital signature is meant to prove a message came from a particular sender; neither can anyone impersonate the sender nor can the sender deny having sent the message. This is useful for example when making an electronic purchase of shares, allowing the receiver to prove who requested the purchase. Digital signatures do not provide confidentiality for the message being sent.

The message is signed using the sender's private signing key. The digitally signed message is then sent to the receiver, who can then use the sender's public key to verify the signature.

Certification authority

In order for Enveloped Public Key Encryption to be as secure as possible, there needs to be a "gatekeeper" of public and private keys, or else anyone could create key pairs and masquerade as the intended sender of a communication, proposing them as the keys of the intended sender. This digital key "gatekeeper" is known as a certification authority. A certification authority is a trusted third party that can issue public and private keys, thus certifying public keys. It also works as a depository to store key chain and enforce the trust factor.

Postal analogies

An analogy that can be used to understand the advantages of an asymmetric system is to imagine two people, Alice and Bob, who are sending a secret message through the public mail. In this example, Alice wants to send a secret message to Bob, and expects a secret reply from Bob.

With a symmetric key system, Alice first puts the secret message in a box, and locks the box using a padlock to which she has a key. She then sends the box to Bob through regular mail. When Bob receives the box, he uses an identical copy of Alice's key (which he has somehow obtained previously, maybe by a face-to-face meeting) to open the box, and reads the message. Bob can then use the same padlock to send his secret reply.

In an asymmetric key system, Bob and Alice have separate padlocks. First, Alice asks Bob to send his open padlock to her through regular mail, keeping his key to himself. When Alice receives it, she uses it to lock a box containing her message, and sends the locked box to Bob. Bob can then unlock the box with his key and read the message from Alice. To reply, Bob must similarly get Alice's open padlock to lock the box before sending it back to her.

The critical advantage in an asymmetric key system is that Bob and Alice never need to send a copy of their keys to each other. This prevents a third party – perhaps, in this example, a corrupt postal worker who opens unlocked boxes – from copying a key while it is in transit, allowing the third party to spy on all future messages sent between Alice and Bob. In addition, if Bob were careless and allowed someone else to copy his key, Alice's messages to Bob would be compromised, but Alice's messages to other people would remain secret, since the other people would be providing different padlocks for Alice to use.

Another kind of asymmetric key system, called a three-pass protocol, requires neither party to even touch the other party's padlock (or key to get access); Bob and Alice have separate padlocks. First, Alice puts the secret message in a box, and locks the box using a padlock to which only she has a key. She then sends the box to Bob through regular mail. When Bob receives the box, he adds his own padlock to the box, and sends it back to Alice. When Alice receives the box with the two padlocks, she removes her padlock and sends it back to Bob. When Bob receives the box with only his padlock on it, Bob can then unlock the box with his key and read the message from Alice. Note that, in this scheme, the order of decryption is NOT the same as the order of encryption – this is only possible if commutative ciphers are used. A commutative cipher is one in which the order of encryption and decryption is interchangeable, just as the order of multiplication is interchangeable (i.e., A*B*C = A*C*B = C*B*A). This method is secure for certain choices of commutative ciphers, but insecure for others (e.g., a simple XOR). For example, let E1() and E2() be two encryption functions, and let "M" be the message so that if Alice encrypts it using E1() and sends E1(M) to Bob. Bob then again encrypts the message as E2(E1(M)) and sends it to Alice. Now, Alice decrypts E2(E1(M)) using E1(). Alice will now get E2(M), meaning when she sends this again to Bob, he will be able to decrypt the message using E2() and get "M". Although none of the keys were ever exchanged, the message "M" may well be a key (e.g., Alice's Public key). This three-pass protocol is typically used during key exchange.

Actual algorithms: two linked keys

Not all asymmetric key algorithms operate in this way. In the most common, Alice and Bob each own two keys, one for encryption and one for decryption. In a secure asymmetric key encryption scheme, the private key should not be deducible from the public key. This makes possible public key encryption, since an encryption key can be published without compromising the security of messages encrypted with that key.

In other schemes, either key can be used to encrypt the message. When Bob encrypts a message with his private key, only his public key will successfully decrypt it, authenticating Bob's authorship of the message. In the alternative, when a message is encrypted with the public key, only the private key can decrypt it. In this arrangement, Alice and Bob can exchange secret messages with no prior secret agreement, each using the other's public key to encrypt, and each using their own private key to decrypt.

Weaknesses

Among symmetric key encryption algorithms, only the one-time pad can be proven to be secure against any adversary – no matter how much computing power is available. However, there is no public key scheme with this property, since all public key schemes are susceptible to a "brute-force key search attack". Such attacks are impractical if the amount of computation needed to succeed – termed the "work factor" by Claude Shannon – is out of reach of all potential attackers. In many cases, the work factor can be increased by simply choosing a longer key. But other algorithms may have much lower work factors, making resistance to a brute-force attack irrelevant. Some special and specific algorithms have been developed to aid in attacking some public key encryption algorithms – both RSA and ElGamal encryption have known attacks that are much faster than the brute-force approach. These factors have changed dramatically in recent decades, both with the decreasing cost of computing power and with new mathematical discoveries.

Aside from the resistance to attack of a particular key pair, the security of the certification hierarchy must be considered when deploying public key systems. Some certificate authority – usually a purpose-built program running on a server computer – vouches for the identities assigned to specific private keys by producing a digital certificate. Public key digital certificates are typically valid for several years at a time, so the associated private keys must be held securely over that time. When a private key used for certificate creation higher in the PKI server hierarchy is compromised, or accidentally disclosed, then a "man-in-the-middle attack" is possible, making any subordinate certificate wholly insecure.

Major weaknesses have been found for several formerly promising asymmetric key algorithms. The 'knapsack packing' algorithm was found to be insecure after the development of a new attack. Recently, some attacks based on careful measurements of the exact amount of time it takes known hardware to encrypt plain text have been used to simplify the search for likely decryption keys (see "side channel attack"). Thus, mere use of asymmetric key algorithms does not ensure security. A great deal of active research is currently underway to both discover, and to protect against, new attack algorithms.

Another potential security vulnerability in using asymmetric keys is the possibility of a "man-in-the-middle" attack, in which the communication of public keys is intercepted by a third party (the "man in the middle") and then modified to provide different public keys instead. Encrypted messages and responses must also be intercepted, decrypted, and re-encrypted by the attacker using the correct public keys for different communication segments, in all instances, so as to avoid suspicion. This attack may seem to be difficult to implement in practice, but it is not impossible when using insecure media (e.g., public networks, such as the Internet or wireless forms of communications) – for example, a malicious staff member at Alice or Bob's Internet Service Provider (ISP) might find it quite easy to carry out. In the earlier postal analogy, Alice would have to have a way to make sure that the lock on the returned packet really belongs to Bob before she removes her lock and sends the packet back. Otherwise, the lock could have been put on the packet by a corrupt postal worker pretending to be Bob, so as to fool Alice.

One approach to prevent such attacks involves the use of a certificate authority, a trusted third party responsible for verifying the identity of a user of the system. This authority issues a tamper-resistant, non-spoofable digital certificate for the participants. Such certificates are signed data blocks stating that this public key belongs to that person, company, or other entity. This approach also has its weaknesses – for example, the certificate authority issuing the certificate must be trusted to have properly checked the identity of the key-holder, must ensure the correctness of the public key when it issues a certificate, must be secure from computer piracy, and must have made arrangements with all participants to check all their certificates before protected communications can begin. Web browsers, for instance, are supplied with a long list of "self-signed identity certificates" from PKI providers – these are used to check the bona fides of the certificate authority and then, in a second step, the certificates of potential communicators. An attacker who could subvert any single one of those certificate authorities into issuing a certificate for a bogus public key could then mount a "man-in-the-middle" attack as easily as if the certificate scheme were not used at all. In an alternate scenario rarely discussed, an attacker who penetrated an authority's servers and obtained its store of certificates and keys (public and private) would be able to spoof, masquerade, decrypt, and forge transactions without limit.

Despite its theoretical and potential problems, this approach is widely used. Examples include SSL and its successor, TLS, which are commonly used to provide security for web browser transactions (for example, to securely send credit card details to an online store).

Computational cost

The public key algorithms known thus far are relatively computationally costly compared with most symmetric key algorithms of apparently equivalent security. The difference factor is the use of typically quite large keys. This has important implications for their practical use. Most are used in hybrid cryptosystems for reasons of efficiency – in such a cryptosystem, a shared secret key ("session key") is generated by one party, and this much briefer session key is then encrypted by each recipient's public key. Each recipient then uses his own private key to decrypt the session key. Once all parties have obtained the session key, they can use a much faster symmetric algorithm to encrypt and decrypt messages. In many of these schemes, the session key is unique to each message exchange, being pseudo-randomly chosen for each message.

Associating public keys with identities

The binding between a public key and its "owner" must be correct, or else the algorithm may function perfectly and yet be entirely insecure in practice. As with most cryptography applications, the protocols used to establish and verify this binding are critically important. Associating a public key with its owner is typically done by protocols implementing a public key infrastructure – these allow the validity of the association to be formally verified by reference to a trusted third party in the form of either a hierarchical certificate authority (e.g., X.509), a local trust model (e.g., SPKI), or a web of trust scheme, like that originally built into PGP and GPG, and still to some extent usable with them. Whatever the cryptographic assurance of the protocols themselves, the association between a public key and its owner is ultimately a matter of subjective judgment on the part of the trusted third party, since the key is a mathematical entity, while the owner – and the connection between owner and key – are not. For this reason, the formalism of a public key infrastructure must provide for explicit statements of the policy followed when making this judgment. For example, the complex and never fully implemented X.509 standard allows a certificate authority to identify its policy by means of an object identifier, which functions as an index into a catalog of registered policies. Policies may exist for many different purposes, ranging from anonymity to military classifications.

Relation to real world events

A public key will be known to a large and, in practice, unknown set of users. All events requiring revocation or replacement of a public key can take a long time to take full effect with all who must be informed (i.e., all those users who possess that key). For this reason, systems that must react to events in real time (e.g., safety-critical systems or national security systems) should not use public key encryption without taking great care. There are four issues of interest:

Privilege of key revocation

A malicious (or erroneous) revocation of some (or all) of the keys in the system is likely, or in the second case, certain, to cause a complete failure of the system. If public keys can be revoked individually, this is a possibility. However, there are design approaches that can reduce the practical chance of this occurring. For example, by means of certificates, we can create what is called a "compound principal" – one such principal could be "Alice and Bob have Revoke Authority". Now, only Alice and Bob (in concert) can revoke a key, and neither Alice nor Bob can revoke keys alone. However, revoking a key now requires both Alice and Bob to be available, and this creates a problem of reliability. In concrete terms, from a security point of view, there is now a "single point of failure" in the public key revocation system. A successful Denial of Service attack against either Alice or Bob (or both) will block a required revocation. In fact, any partition of authority between Alice and Bob will have this effect, regardless of how it comes about.

Because the principle allowing revocation authority for keys is very powerful, the mechanisms used to control it should involve both as many participants as possible (to guard against malicious attacks of this type), while at the same time as few as possible (to ensure that a key can be revoked without dangerous delay). Public key certificates that include an expiration date are unsatisfactory in that the expiration date may not correspond with a real-world revocation but at least such certificates need not all be tracked down system-wide, nor must all users be in constant contact with the system at all times.

Distribution of a new key

After a key has been revoked or when a new user is added to a system, a new key must be distributed in some predetermined manner. Assume that Carol's key has been revoked. Until a new key has been distributed, no one will be able to send her messages and messages from her cannot be signed without violating system protocols (i.e., without a valid public key, no one can encrypt messages to her).

One could leave the power to create, certify, and revoke keys in the hands of each user, as the original PGP design did, but this raises problems of user understanding and operation. For security reasons, this approach has considerable difficulties – if nothing else, some users could be forgetful, inattentive, or confused. On the one hand, a message revoking a public key certificate should be spread as fast as possible, while on the other hand, parts of the system might be rendered inoperable before a new key can be installed. The time window can be reduced to zero by always issuing the new key together with the certificate that revokes the old one, but this requires co-location of authority to both revoke keys and generate new keys.

It is most likely a system-wide failure if the (possibly combined) principal that issues new keys fails by issuing keys improperly. This is an instance of a "common mutual exclusion" – a design can make the reliability of a system high, but only at the cost of system availability (and vice versa).

Spreading the revocation

Notification of a key certificate revocation must be spread to all those who might potentially hold it, and as rapidly as possible.

There are but two means of spreading information (i.e., a key revocation) in a distributed system: either the information is "pushed" to users from a central point (or points), or else it is "pulled" from a central point (or points) by the end users.

Pushing the information is the simplest solution, in that a message is sent to all participants. However, there is no way of knowing whether all participants will actually receive the message. If the number of participants is large, and some of their physical or network distances are great, then the probability of complete success (which is, in ideal circumstances, required for system security) will be rather low. In a partly updated state, the system is particularly vulnerable to "denial of service" attacks as security has been breached, and a vulnerability window will continue to exist as long as some users have not "gotten the word". Put another way, pushing certificate revocation messages is neither easy to secure, nor very reliable.

The alternative to pushing is pulling. In the extreme, all certificates contain all the keys needed to verify that the public key of interest (i.e., the one belonging to the user to whom one wishes to send a message, or whose signature is to be checked) is still valid. In this case, at least some use of the system will be blocked if a user cannot reach the verification service (i.e., one of the systems that can establish the current validity of another user's key). Again, such a system design can be made as reliable as one wishes, at the cost of lowering security – the more servers to check for the possibility of a key revocation, the longer the window of vulnerability.

Another trade-off is to use a somewhat less reliable, but more secure, verification service, but to include an expiration date for each of the verification sources. How long this "timeout" should be is a decision that requires a trade-off between availability and security that will have to be decided in advance, at the time of system design.

Recovery from a leaked key

Assume that the principal authorized to revoke a key has decided that a certain key must be revoked. In most cases, this happens after the fact – for instance, it becomes known that at some time in the past an event occurred that endangered a private key. Let us denote the time at which it is decided that the compromise occurred as T.

Such a compromise has two implications. First, messages encrypted with the matching public key (now or in the past) can no longer be assumed to be secret. One solution to avoid this problem is to use a protocol that has perfect forward secrecy. Second, signatures made with the no-longer-trusted-to-be-actually-private key after time T can no longer be assumed to be authentic without additional information (i.e., who, where, when, etc.) about the events leading up to the digital signature. These will not always be available, and so all such digital signatures will be less than credible. A solution to reduce the impact of leaking a private key of a signature scheme is to use timestamps.

Loss of secrecy and/or authenticity, even for a single user, has system-wide security implications, and a strategy for recovery must thus be established. Such a strategy will determine who has authority to, and under what conditions one must, revoke a public key certificate. One must also decide how to spread the revocation, and ideally, how to deal with all messages signed with the key since time T (which will rarely be known precisely). Messages sent to that user (which require the proper – now compromised – private key to decrypt) must be considered compromised as well, no matter when they were sent.

Examples

Examples of well-regarded asymmetric key techniques for varied purposes include:

• Diffie–Hellman key exchange protocol
• DSS (Digital Signature Standard), which incorporates the Digital Signature Algorithm
• ElGamal
• Various elliptic curve techniques
• Various password-authenticated key agreement techniques
• Paillier cryptosystem
• RSA encryption algorithm (PKCS#1)
• Cramer–Shoup cryptosystem
• YAK authenticated key agreement protocol

Examples of asymmetric key algorithms not widely adopted include:

• NTRUEncrypt cryptosystem
• McEliece cryptosystem

Examples of notable – yet insecure – asymmetric key algorithms include:

• Merkle–Hellman knapsack cryptosystem

Examples of protocols using asymmetric key algorithms include:

• S/MIME
• GPG, an implementation of OpenPGP
• Internet Key Exchange
• PGP
• ZRTP, a secure VoIP protocol
• Secure Socket Layer, now codified as the IETF standard Transport Layer Security (TLS)
• SILC
• SSH
• Bitcoin
• Off-the-Record Messaging

See also

Some use of "" in your query was not closed by a matching "".Some use of "" in your query was not closed by a matching "".

• Books on cryptography
• GNU Privacy Guard
• ID-based encryption (IBE)
• Key escrow
• Key-agreement protocol
• PGP word list
• Pretty Good Privacy
• Pseudonymity
• Public key fingerprint
• Public key infrastructure (PKI)
• Quantum computing
• Quantum cryptography
• Secure Shell (SSH)
• Secure Sockets Layer (SSL)
• Symmetric-key algorithm
• Threshold cryptosystem

References

• Hirsch, Frederick J. "SSL/TLS Strong Encryption: An Introduction". Apache HTTP Server. Retrieved 2013-04-17.. The first two sections contain a very good introduction to public-key cryptography.
• Ferguson, Niels; Schneier, Bruce (2003). Practical Cryptography. Wiley. ISBN 0-471-22357-3. Search this book on
• Katz, Jon; Lindell, Y. (2007). Introduction to Modern Cryptography. CRC Press. ISBN 1-58488-551-3. Search this book on
• Menezes, A. J.; van Oorschot, P. C.; Vanstone, Scott A. (1997). Handbook of Applied Cryptography. ISBN 0-8493-8523-7. Search this book on
• IEEE 1363: Standard Specifications for Public-Key Cryptography
• Christof Paar, Jan Pelzl, "Introduction to Public-Key Cryptography", Chapter 6 of "Understanding Cryptography, A Textbook for Students and Practitioners". (companion web site contains online cryptography course that covers public-key cryptography), Springer, 2009.

External links

• Oral history interview with Martin Hellman, Charles Babbage Institute, University of Minnesota. Leading cryptography scholar Martin Hellman discusses the circumstances and fundamental insights of his invention of public key cryptography with collaborators Whitfield Diffie and Ralph Merkle at Stanford University in the mid-1970s.
• An account of how GCHQ kept their invention of PKE secret until 1997

📰 Article(s) of the same category(ies)

• SAFE-BioPharma Association
• Digital currency
• Zain Cash
• Ferratum Group
• X Certificate and Key management
• List of Issuer Identification Numbers
• Holvi

---