Hyper-Spherical Search Algorithm
Hyper-Spherical Search Algorithm (HSS)[1] is an optimization algorithm which is used as a computational method to solve non-linear optimization problems for different aspects, in computer science. Similar to the most optimization algorithms, HSS does not need the gradient of the objective function in its process.
Most non-linear optimization problems appearing in different areas of science, management and engineering cannot be analytically solved. Different approaches and interesting techniques have emerged and some of their applications have been reported, e.g., drug design, music composition, and financial forecasting. Evolutionary Algorithms (EAs) are more successful than other optimization techniques. In this group, the Genetic Algorithm (GA), Particle Swarm Optimization (PSO) and Harmony Search Algorithm (HSA) are applied to solve the optimization problems.[2][3]
HSS algorithm is proposed to solve optimization of the non-linear mixed-integer problems. The proposed method, Like other evolutionary algorithms, starts with an initial population. Population individuals are of two types: particles and hyper-sphere centers that all together form particle sets.[1] Searching the hyper-sphere inner space made by the hyper-sphere center and its particle is the basis of the proposed evolutionary algorithm. The HSS algorithm hopefully converges to a state at which there exists only one hyper-sphere center (SC) and its particles are at the same position and have the same cost function value as the hyper-sphere center. Applying the proposed algorithm to some benchmark cost functions, shows its ability in dealing with different types of optimization problems. The HSS has been compared with GA, HSA and PSO for mathematical problems in HSS paper,[1] and with ICA and HSA in an engineering problem which show better speed and convergence to achieve optimal point (more info,more info).
The source code of this algorithm in MATLAB coding language can be accessed in here. Extra information can be found at the personal page of Hossein Karami.
Algorithm[edit]
The HSS algorithm procedure is divided into five steps as follows:
Step 1: Particles initialization[4][edit]

This step initializes the algorithm and includes the following four sub-steps:
- Parameters initialization: set the algorithm parameters by the user.
- Generation of initial population: Randomly generating initial set with a uniform probability
- Hyper-sphere center nomination: the best particles are selected to be the SCs.
- Particles distribution among hyper-spheres: particles are distributed among SCs considering the SCs dominance, which is inversely proportional to their objective function values.
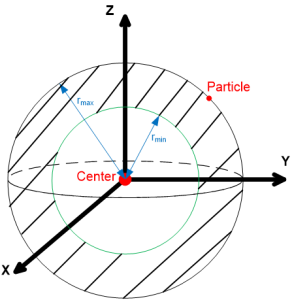
Step 2: Searching[4][edit]

The searching procedure will be carried out by changing the parameters of the particle in spherical coordinates, i.e., r and θ. Each angle of a particle is changed by α radians with the probability of Prangle. The α is randomly selected in each iteration between (0, 2π) with a uniform distribution. After changing the angle(s) of particles, the distance between the particle and the center is randomly selected between it (Fig.1).
The possible position of a particle is illustrated by the dashed space for a 3-D case (Fig. 2). The search procedure is a transformation, which changes the position of a particle (or SC).
Step 3: Dummy Particle Recovery[5][edit]
Each SC and its corresponding particles make a set of particles. Among all the particles, some of them have the largest value of the objective function (cost) and it is not expected that they reach the global minimum value of the objective function. In other words, these particles (dummy particles) search the inappropriate space and therefore, their searching hyper-spheres should be changed. In this step, the dummy particles are assigned to other SCs.
Step 4: Determining New Particles and SCs[5][edit]
After particle search in its sphere, a particle may reach a position with lower objective function value than its corresponding SC. This event may be seen after each search and the position of the SC and the particle are exchanged.
Step 5: Convergence Testing[6][edit]
After a while, all the SCs except the best one will be eliminated and all the particles will be assigned to the best SC. In this condition, there is almost no difference between this SC and the particles. The algorithm is terminated if one of the following conditions is reached:
a) The maximum number of iterations is reached (for example 1000 iterations).
b) The percentage of difference between the best SCs in two consequential iterations becomes lower than a preset threshold (e.g., 10−6).
References[edit]
- ↑ 1.0 1.1 1.2 Karami, Hossein; Sanjari, Mohammad-Javad; Gharehpetian, Gevork B. (November 2014). "Hyper-Spherical Search (HSS) algorithm: a novel meta-heuristic algorithm to optimize nonlinear functions". Neural Computing and Applications. 25 (6): 1455–1465.
- ↑ Karami, Hossein; Sanjari, Mohammad-Javad; Hosseinian, S.Hossein; Gharehpatian, Gevork B. (2014). "An Optimal Dispatch Algorithm for Managing Residential Distributed Energy Resources". IEEE Transactions on Smart Grid. 5 (5): 2360–2367.
- ↑ Karami, Hossein; Sanjari, Mohammad-Javad; Tavakoli, Atrin; Gharehpatian, Gevork B. (2013). "Optimal Scheduling of Residential Energy System Including Combined Heat and Power System and Storage Device". Electric Power Components and Systems. 41 (8): 765–781.
- ↑ 4.0 4.1 Ahmadi, Seyed-Alireza; Karami, Hossein; Sanjari, Mohammad-Javad; Tarimoradi, Hadi; Gharehpatian, Gevork B. (2016). "Application of hyper-spherical search algorithm for optimal coordination of overcurrent relays considering different relay characteristics". International Journal of Electrical Power & Energy Systems. 83: 443–449.
- ↑ 5.0 5.1 Sanjari, Mohammad-Javad; Karami, Hossein; Abdolhalim, Yatim; Gharehpatian, Gevork B. (2015). "Application of Hyper-Spherical Search algorithm for optimal energy resources dispatch in residential microgrids". Applied Soft Computing. 37: 15–23.
- ↑ "Personal Page of Hossein Karami".
This article "Hyper-Spherical Search Algorithm" is from Wikipedia. The list of its authors can be seen in its historical. Articles copied from Draft Namespace on Wikipedia could be seen on the Draft Namespace of Wikipedia and not main one.
